What is the purpose of a test of hypothesis?
A hypothesis test is a decision-making process that examines a set or sets of data, and on the basis of expectation under null hypotheses, leads to a decision as to whether or not to reject null hypotheses. Because in many circumstances we merely wish to know whether a certain proposition is true or false. The process of hypothesis tests provides a framework for making decisions on an objective basis, by weighing the relative merits of different hypotheses, rather than on a subjective basis by simply looking at the numbers. Different people can form differnt opinions by looking at data (confounded by chance variation or sampling errors), but a hypothesis test provides a standardized decision-making process that will be consistent for all people
Does hypothesis test ever prove a null hypothesis
When the probability is greater than 0.05 levels, we reject the experimental hypothesis. However this does not mean that the null hypothesis (no effect in the population) is true. Non-significant test results tell us that the effect is not big enough to be anything other than a chance finding and doesn’t tell us the effect is 0. As Cohen (1990), points out, non-significant results never be interpreted as ‘no’ difference between means ‘or’ no relationship between variables. He further points out that the null hypothesis is never true because from sampling distribution that two random samples will have slightly different means and even though these differences can be small, they are nevertheless different. Even small differences would be deemed as statistically significant if a larger sample size were used. So, hypothesis or significance testing can ever tell us that the null hypothesis is true.
What is a p value? What does the p-value mean in words?
The p value is the probability of getting values of the test statistics as extreme as or more extreme than, that observed if the null hypothesis is true. The p-value is usually compared to the predetermined significance level α to decide whether the null hypothesis should be rejected or not. In general, small p-value or p value less than or equal to α, we reject H0 while a large p-value or p is greater than α, we do not reject H0 or no evidence against null hypothesis. Many writers, when reporting conclusion in the research, prefer to report findings in terms of p values to report whether that an observed value of the test statistical significant
Briefly explain the relationship between confidence interval and hypothesis testing?
Solution: There exist close relationship between confidence interval and hypotheses testing. When constructing of 95% confidence interval, all values in the interval are considered plausible for the parameter being estimated. The values outside this interval are rejected as relatively implausible. If the value of the parameter specified by the null hypotheses is contained in the 95% interval then the null hypothesis cannot be rejected at the level of 0.05 levels. If the value specified by the null hypothesis is not in the interval then the null hypothesis can be rejected at the 0.05 level. If a 99% confidence interval is constructed, then values outside the interval are rejected at the 0.01 level.
Under what circumstances might you use a one-sided test of hypothesis rather than a two-sided test?
When the alternate hypothesis does specify a direction, then one-sided test of hypothesis could be used. In general a one sided test hypothesis is appropriate when a large difference in one direction would lead to the same action as no difference at all.
Explain the analogy between type 1 and the type II errors in a test of hypothesis and the false positive and false negative results that occur in diagnostic testing.
Type 1 error or rejection error or an α error occurs when we believe that there is a genuine effect in our population, when in fact there isn’t or A type 1 error is made if we reject the null hypothesis when H0 is true and the probability of making type 1 error is determined by the significance level (Fisher’s Criterion = 0.05 or 5% chance) of the test. The opposite is a Type II error or a β error or acceptance, which occurs when we believe that there is no effect in the population when, in reality, there is or it is made if we fail to reject the hull hypothesis when H0 is false. These errors are made during decision process in statistics.
The false positive that occurs in diagnostic testing is also known as Type 1 errors and false negative is also called as Type II error or β error.
The distribution of diastolic blood pressure for the population of female diabetics between the ages of 30 and 34 has an unknown mean Ud and standard deviation = 9.1mmHg. It may be useful to physicians to know whether the mean of this population is equal to the mean diastolic blood pressure of the general population of females in this age group, 74.4 mmHg?
Solution: The mean diastolic blood pressure of the female diabetics between the ages of 30 and 34 is equal to the mean of the general population of females in the same age group. H0: µ = µ0 = 74.4mmHg
Solution: The mean diastolic blood pressure of the female diabetics between the ages of 30 and 34 is not equal to the mean of the general population of females in the same age group. HA: µ ≠ µ0 = 74.4mmHg
A sample of ten diabetic women is selected; their mean diastolic blood pressure is =84 mmHg. Using this information, conduct a two-sided test and the alpha level = 0.05 level of significance. What is the p-value of the test?
- To compute the test statistics, we use the below formula to calculate the p value, Z = x - µ0 / / √n = 84-74.4 / 9.1 / √10 = 3.33
- Z value = 3.33
- P value of the test (at alpha level 0.05 level of significance), p <0.0001
What conclusion do you draw from the results of the test?
Based on the above value, we can conclude that the mean diastolic blood pressure of the diabetic women is significantly different from the population mean diastolic blood pressure (74.4mmHg) of females in the same age group. Hence we reject null hypothesis.
Would your conclusion have been different if you had chosen alpha=0.01 instead of alpha= 0.05?
No my conclusion would not be different, even if I had chosen alpha = 0.01 instead of alpha = 0.05, since the difference observed is considered to be extremely statistically significant.
E.Canis infection is a tick-borne disease of dogs that is sometimes contracted by humans. Among infected humans, the distribution of white blood cells count has an unknown mean and a standard deviation. In the general population, the mean white blood cell count is 7250/mm3. It is believed that persons infected with E.Canis must on average have lower white blood cell counts.
Null hypothesis: The mean white blood cells of the persons infected with E,Canis will be lower than that of mean of general population, The null hypothesis for the test is, H0: µ ≥ 7250/mm3
Z = x - µ0 / / √n = 4767 – 7250 / 3204 √15 = -2.999
Z = -2.999, p value = 0.001.
What do you conclude?
From the above results, sine p value is smaller than α = 0.05, we reject the null hypothesis and state that, the mean of white blood cells of the persons infected with E,Canis was lower than the that of mean of general population.
What is the probability of making a type 1 error?
In this case, we know that the null hypothesis is false, since the serum cholesterol level of the men who do not develop heart diseases cannot be higher than the mean level for men who do. If the tests of hypothesis lead us to accept H0, saying that there is no difference between the mean cholesterol, then we increase the probability of making a type 1 error.
If a sample of size 25 is selected from the population of men who do not go on to develop coronary heart diseases, what is the probability of making a type II error?
Z = x - µ0 / / √n = 219-244 / 25 √25 = -3.05
P value =0.001.
In this case, the sample mean is less than the population mean. Therefore, the probability of failing to reject null hypothesis, given that null hypothesis is false (sample mean = 219mg/100 ml and population mean =244mg/100 ml)
What is the power of the test?
β = 1 – 0.001 = 0.999. There is a 99.9% chance of rejecting the null hypothesisHow could you increase the power?
What is the main difference between paired and independent samples?
PairedIn paired sample, the sample is matched to a unique data point in the second sample, among the same population. Independent samples consider two or unrelated separate groups.
Explain the purpose of paired data. In certain situations, what might be the advantage of using paired samples rather than independent ones?
Paired t test are used to compare means on the same or related subject over time or in differing circumstances. The observed data are from the same subject or from a matched subject and are drawn from a population with a normal distribution. Subjects are often tested in a before-after situation (across time, with some intervention occurring such as a diet), or subjects are paired such as with twins, or with subject as alike as possible.
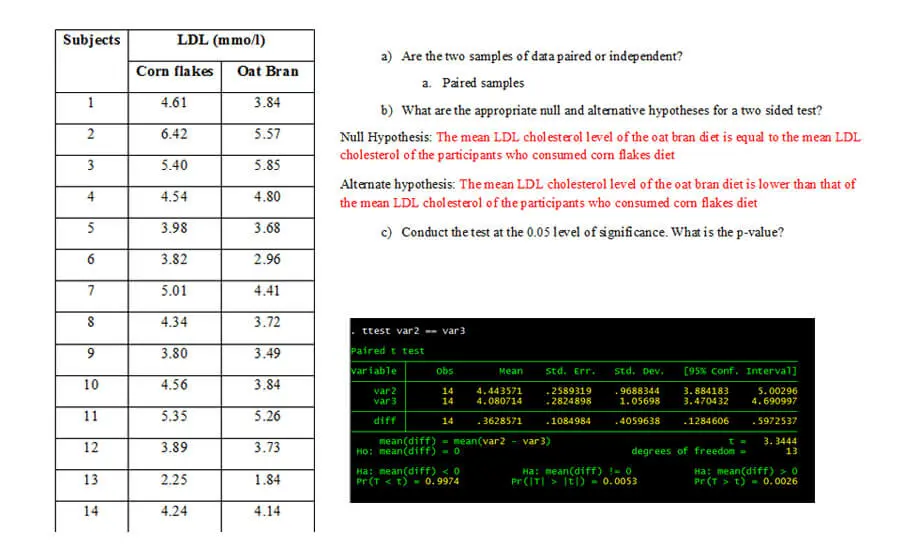
A crossover study was conducted to investigate whether oat bran cereal helps to lower serum cholesterol levels in hypercholestermic males. 14 such individuals were randomly placed on a diet that included either oat bran or corn flakes; after two weeks, their low density lipoprotein (LDL) cholesterol levels were recorded. Each man was then switched to the alternative diet. After a second two week period, the LDL cholesterol level of each individual was again recorded. The data from this study are shown below