Multiplicity Problem in Clinical Trials and Some Statistical Approaches
November 19, 2019
Evaluation of autoregressive time series prediction using validity of cross-validation
November 30, 2019The problem with unadjusted multiple and sequential statistical testing
The problem with unadjusted multiple and sequential statistical testing
In most Statistical Analysis, researchers often wish to get sufficient power to balance the cost spent for the experiment such as in medical experiment. The most common statistical technique is that using sequential sampling of data until the desired condition is satisfied. However, using this technique leads to an inflated rate of type I and type II error rate. In this blog, the Statistical Method which deals with the sequential sampling procedure are discussed.
When a large number of statistical tests are performed, then there will be a chance of increased false positive rates or there will be the problem of multiple testing for the sample considered. Usually, Bonferroni correction will be carried out to deal with the multiple testing problems without making any adjustments.
But, this Bonferroni correction have serious drawback. That is, if we perform multiple independent tests, then the probability or chance of getting atleast one false positive is calculated as 1-(1-0.05)^n. Suppose if n=10, then the probability will be 40.14 percent, which is very high. In such situations, the use of Bonferroni correction is not appropriate.
Sequential testing problem is an alternative to cope up with the multiple testing problems. Sequential testing means the researchers collect the data until we reach the fixed threshold. But it takes more effort, time and it’s expensive in practice. Also, one can check the decreasing p-value when the samples are tested sequentially.
In an uncorrected multiple testing procedure, one would impose the stopping rule, say, stop the process once the false positive rate reaches 25%. In such case, the chance of getting significant results will be one in four. Although this procedure seems comfortable, it will have an impact on the estimated values. In the same way, sequential testing problem have a serious drawback. That is, when we do sampling sequentially, researchers often face an effect of over estimates. Thus, effect size is also result in bias nature.
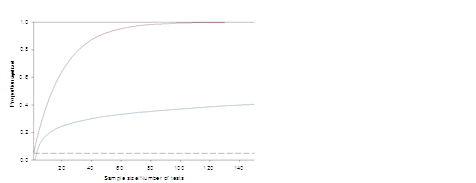
Look at the figure below, this figure explains the severity of the problem of sequential and multiple testing. The following figure explains the Sample Size Significance for the simulated 10000 sequential strategies. From the graph, it is noted that the sequential testing (blue curve) is less severe than the uncorrelated multiple testing (red curve). As explained earlier, if we impose any stopping rule also it will exceed the limit and gives a false discovery rate.
However, this kind of testing affects the estimated values apart from the probability values. Because, in sequential sampling, distance between both group means will increase or decrease and if one wish to continue the process of sampling till both groups yields significant results, then it may lead to overestimation. Hence, the sequential testing is biased in significance and also in effect size.
So far, I have mentioned about the problem of unadjusted sequential testing. The concept of sequential testing is actually a great idea only if we make necessary corrections to make the sample to be larger in size. Because, if we sample the data sequentially in smaller bits and achieve the fixed limit means we actually increasing the sample size to attain our goal. To handle these situations, there are two classes of approaches available in literature. They are : group sequential analysis and full Sequential Analysis.
In a group sequential analysis or interim analysis the researcher have to make an priori specifications about the data. For instance, one should make the prior decision that the samples should be taken as 50 samples in first level, 100 in second level, etc., and stops when the desired result is obtained. The main advantage of this technique is that one can stop the Data Collection when the desired level is obtained.
Whereas in the full sequential technique, there is no prior arrangements is needed. In early 1940s, Walds used this technique in computing the cumulative log-likelihood ratio for each observation collected and stops the process when a pre-defined threshold is achieved. This is something like the case in Interim Analysis. However, the full sequential technique is not practical. Suppose if a researcher wants to analyse the sample of 20 group therapy participants, then this may not be appropriate but the group sequential analysis will serves a purpose.
To conclude, i will make a note on various approaches to handle multiple testing problem.
With this note, I end up this blog about the problem of unadjusted multiple testing and sequential testing procedures. To know more about these please refer literatures in the references below.
References
- John, L. K., Loewenstein, G. & Prelec, D. Measuring the prevalence of Questionable Research Practices with incentives for truth telling. Psychol. Sci. 23, 524–532 (2012).
- Fiedler, K. & Schwarz, N. Questionable research practices revisited. Soc. Psychol. Pers. Sci. 7, 45–52 (2015).
- Benjamin et al. Redefine statistical significance. Nat. Hum. Behav. 2, 6–10 (2018).
- Lakens, D. et al. Justify your alpha. Nat. Hum. Behav. 2, 168–171 (2018).
- Althouse, A. Adjust for multiple comparisons? It’s not that simple. Ann. Thorac. Surg. 101(5), 1644–1645 (2016).
- Bender, R. & Lange, S. Adjusting for multiple testing – when and how? J. Clin. Epidemiol. 54, 343–349 (2001).
- Fiedler, K., Kutzner, F. & Krueger, J. I. The long way from α-error control to validity proper: problems with a short-sighted false-positive debate. Pers. Psychol. Sci. 7, 661–669 (2012).
- Wald, A. Sequential tests of statistical hypotheses. Ann. Math. Stat. 16, 117–186 (1945).
- Simmons, J. P., Nelson, L. D. & Simonsohn, U. False-positive psychology:undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychol. Sci. 22, 1359–1366 (2011).
- Altman, D. G. Practical Statistics for Medical Research. (Chapman & Hall, Boca Raton, 1991).
