The problem with unadjusted multiple and sequential statistical testing
November 25, 2019
Model-based clustering using a Bayesian approach for binary panel Probit models with examples
November 30, 2019Evaluation of autoregressive time series prediction using validity of cross-validation
- Home
- Blog
- Evaluation of autoregressive time series prediction using validity of cross-validation
Evaluation of autoregressive time series prediction using validity of cross-validation
This blog discusses a note on the validity of Cross-Validation for evaluating autoregressive Time Series Prediction. Before that, let us understand what is a cross-validation technique and why it is different for Time series Analysis.
Cross-Validation (CV)
Basically, Cross Validation is a validation technique used to explain how well the estimated values from a fitted statistical model will generalize to the explanatory variables under study. For instance, it is used to evaluate the Prediction model with the estimates. In addition, CV is used for tuning the hyperparameters in the model and yield robust performance. There are two most widely used techniques of CV available in literature, they are k-fold cross-validation and hold-out cross-validation.
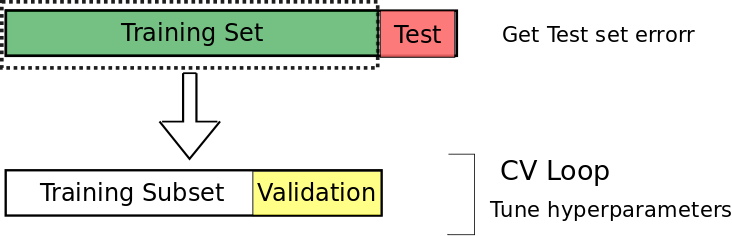
Traditionally, CV technique is performed by splitting the data into training and test set. Suppose, if one need to tune the parameter, then a subset for validation is splitted from the training set. The below figure depicts the same.
Why Cross Validation technique is different for time series data?
The standard procedure for model validation is the K-fold CV as in Regression Analysis and classification problem. However, for predicting the time series data, this K-fold is not a straightforward because of the non-stationarity and serial correlation present in the data. This type of situations often handled by out-of-sample technique of CV (Bergmeir and Benítez, 2012). In addition, the K-fold CV is applicable for the autoregressive models with uncorrelated errors and have wide scope in predicting the model using Machine Learning methods.
Now, lets come to the topic of this blog, Bergmeir et al (2015) discussed the validity of K-fold Cross Validation for time series for purely autoregressive models particularly for the dependent case instead of applying to the independent case and I will bring out the key points discussed in that paper here.
The model selection adopted in that paper is 5-fold Cross Validation using leave-one-out, non-dependent,and out-of-sample evaluation methods using AR(1) to AR(5) models and residuals have been taken care for the uncorrelated errors using Serial Correlation.
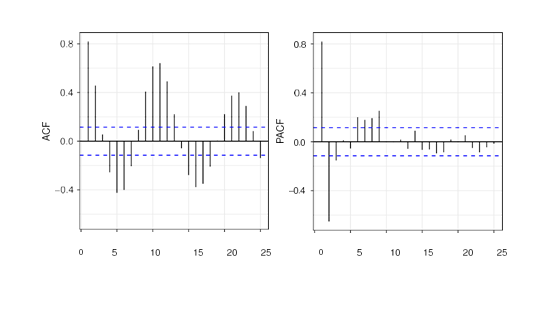
Three different experiments are carried out to forecast the AR model using Monte Carlo simulation. The monthly seasonality from the ACF and PACF plots for the data considered for Monte-Carlo simulation is depicted in the following figure and the results of the experiment is discussed in Bergmeir et al (2015)
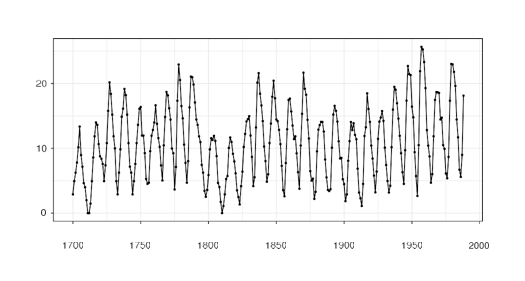
Lets look at the applicability of the procedure using the yearly sun spot data available in R. The data involves 289 observations recorded from 1700 to 1988 and are depicted in the following figure.
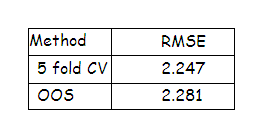
The relevant auto correlation is captured using Ljung-Box test with the residual series of 1560 model configurations. Out of 1560, 763 satisfies the Box test and the configuration which have minimum root mean square error is chosen. The 5-fold CV yields an error rate of 2.247 and out-of-sample (OOS) method yields 2.281 and the CV procedure is not an over fitting model and the results are tabulated below
To sum up, in this blog, we have discussed the applicability of the K-fold Cross Validation procedure for the purely AR models beyond the usual practice and it is found to be useful when the residuals in the model is uncorrelated. From the Monte-Carlo simulation of Bergmeir et al (2015), the K-fold classification yields better result than the common practice of using out-of-sample method for time series data and the real-time data explains the application of this using AR model with uncorrelated errors. The over-fitting and under-fitting of the model is accessed using the Ljung-Box test and it results in there is no such issues occurred in the model. Also, this method examines the applicability of the K-fold cross validation using neural network model with a monte-carlo simulations, and it can also be extended to the other regression models such as random forest and other machine learning techniques. The interesting point is that if we use whatever regression model for these kinds of Time Series Data, this method still proves the K-fold cross validation is the best method. I will leave that for the reader to check whether the same result is obtained for different Statistical Models considered and compare the results with the K-fold cross-validation and out-of-sample method.
See also here
References
- Arlot, S., Celisse, A., 2010. A survey of cross-validation procedures for model selection. Stat. Surv. 4, 40–79.
- Bergmeir, C., Benítez, J.M., 2012. On the use of cross-validation for time series predictor evaluation. Inform. Sci. 191, 192–213.
- Bergmeir, C., Costantini, M., Benítez, J.M., 2014. On the usefulness of cross-validation for directional forecast evaluation. Comput. Statist. Data Anal. 76, 132–143.
- Borra, S., Di Ciaccio, A., 2010. Measuring the prediction error. A comparison of cross-validation, bootstrap and covariance penalty methods. Comput. Statist. Data Anal. 54 (12), 2976–2989.
- Brockwell, P.J., Davis, R.A., 1991. Time Series: Theory and Methods. Springer, New York.
- Budka, M., Gabrys, B., 2013. Density-preserving sampling: Robust and efficient alternative to cross-validation for error estimation. IEEE Trans. Neural Netw. Learn. Syst. 24 (1), 22–34.
- Ljung, G.M., Box, G.E.P., 1978. On a measure of lack of fit in time series models. Biometrika 297–303.
- Christoph Bergmeir & Rob J Hyndman & Bonsoo Koo, 2015. “A Note on the Validity of Cross-Validation for Evaluating Time Series Prediction,” Monash Econometrics and Business Statistics Working Papers 10/15, Monash University, Department of Econometrics and Business Statistics.
