Use Of Machine Learning Algorithms: Accessing World Bank Database & Google Trends To Predict Economic Cycle
January 14, 2020
Research Design Decisions And Be Competent In The Process Of Reliable Data Collection And Analysis
February 4, 2020Panel Data Analysis: A Survey On Model-Based Clustering Of Time Series
Panel Data Analysis: A Survey On Model-Based Clustering Of Time Series
Clustering technique in Statistical Analysis is used to determine the subsets as clusters in the data using specified distance measure. However, this technique cannot be applied easily for longitudinal or time series data. In this blog, I will discuss about some of the methods used for modeling longitudinal or panel data using Clustering Analysis technique as explained in Schmatter (2011).
Longitudinal data is actually a sample of observations which are measured repeatedly over time. And, nowadays, longitudinal/repeated measure data or panel data exists in all areas of Applied statistics such as finance, psychology, economics and social sciences. Most studies deals with analyzing homogeneity in such Time series data (Diggle et al 2002), however, there are few researchers’ shows interest in analyzing the heterogeneity in such data and they proposed different modeling technique for the same. The most common method of capturing the heterogeneity is to assume the presence of latent classes and each class are stratified using the covariates, say, gender and yields aposteriori results whether the stratified classes behaves differently across the time series. This is where the Bayesian paradigms come into play.
Measuring the distance between time series data is not appropriate thus a cluster based modeling strategy for finite mixture models is adopted using Bayesian rule. Model based clustering considers each time series to a single unit contained in an unknown latent class. One can see an excellent review of finite mixture models for longitudinal data in Vermunt (2010) especially in the areas of psychology, bio-statistics and other applied areas.
A common question arise here is to select the choice of prior and the number of clusters. In this paper, the author considered various Bayesian criteria namely, DIC, AIC, BIC, ICL-BIC, and AWE for assessing the model performance and the clustering kernels for the selecting the number of clusters.
Let us now discuss the applicability of the model based clustering technique by means of an example as discussed in Schmatter (2011). The data consists of 237 teenagers who use marijuana for the year 1976-1980. The use marijuana is categorized into three types as never, not more than once a month and more than once a month. This gives an idea that the data contains the categorical variables in this study. The following figure represents the sample of 10 observed response of use of marijuana usage among the 237 teenagers.
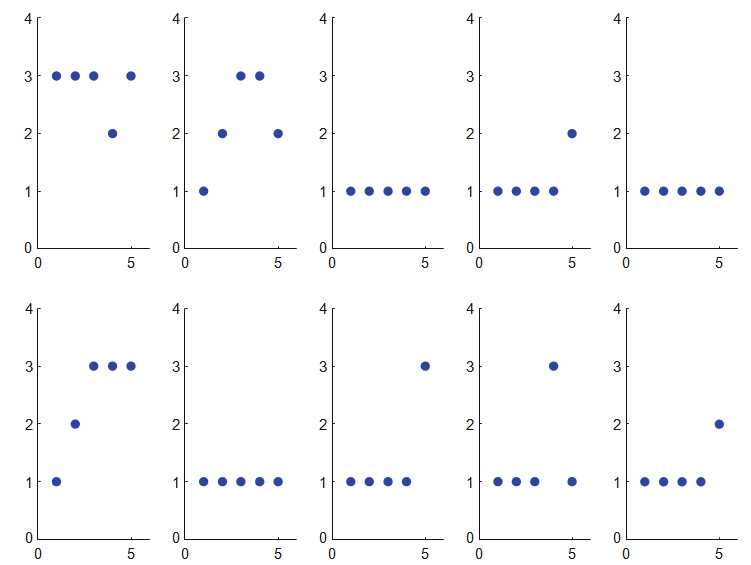
The model considered for analyzing the marijuana usage is based on Generalized transition model. A Dirichlet prior is chosen in this case since the observed response variable is of categorical in nature. Five different kernel classes are considered and evaluated the model using Dirichlet prior distribution and the results for the same is presented in the following table. Various information criteria is adopted to select the number of clusters in this panel study and the best results are marked in bold for easy reference.
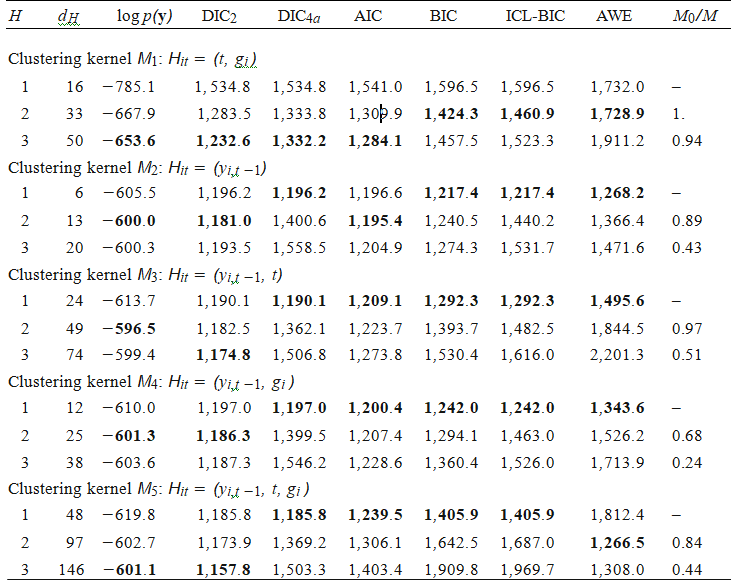
From the above table, it is clear that the clustering kernel M2 to M5 shows that there exists a common behaviour in marijuana usage. Also, the marginal likelihood based clustering technique results in highest value for M3 with two classes. In a similar manner, one can infer the best kernel method for selecting the clusters in different information criteria. In addition, the overfitting of the selection of number of clusters can be assessed using the fraction of M0 by M. If the value is smaller than one, then one may conclude that the method is overfitting, in this case, H3 class of kernel seems to be overfitting. An MCMC simulation is carried out for M3 with H2 and the following figure explains the sample of boxplots of the posterior probabilities for male and female groups.
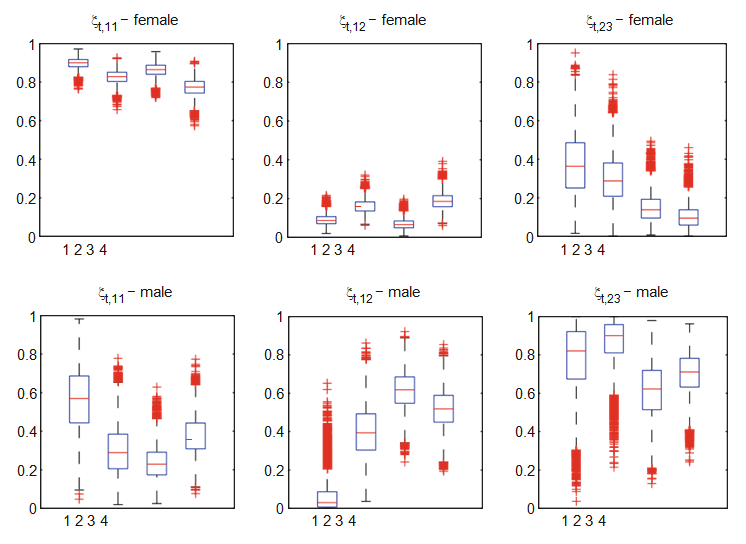
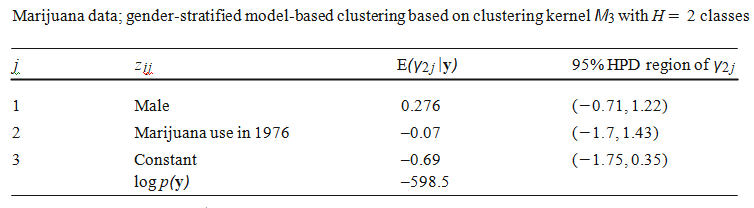
The gender specific posterior inference from the above table shows that male teenager have higher probability than others. Comparing the likelihood results obtained from the above table (598.5) and the previous table (596.5) the stratified Model based clustering reduces to Standard Model based clustering and it is clear that the use of marijuana is not associated with the gender classification. From this results, it is concluded that the use of marijuana among teenagers may be clustered into two with never-use and other being more user groups.
To sum up, model-based clustering technique along with the Bayesian flavor yields better results since it provides an answer to the most troublesome problems in the cluster analysis. In longitudinal or Panel data studies, usage of eculidean distance may be a valid one and hence a kernel based clustering for Time series data Analysis is considered and selection of the best method is analysed usinf different information criteria. In addition to the illustration explained in this paper, an MCMC simulation is carried out to find the optimal clustering methodology. However, this may not be taken as granted for all applications, and a more appropriate method concerning the prior distribution and the choice of kernel is needed in analyzing a time series panel data.
References
- Agresti A (1990) Categorical data analysis. Wiley, Chichester
- Akaike H (1974) A new look at statistical model identification. IEEE Trans Autom Control 19:716–723
- Aßmann C, Boysen-Hogrefe J (2011) A Bayesian approach to model-based clustering for binary panel
- probit models. Comput Stat Data Anal 55:261–279
- Celeux G, Forbes F, Robert CP, Titterington DM (2006) Deviance information criteria for missing data models. Bayesian Anal 1:651–674
- Diggle PJ, Heagerty P, Liang K-Y, Zeger SL (2002) Analysis of longitudinal data, 2nd edn. Oxford Uni- versity Press, Oxford
- Everitt BS (1979) Unresolved problems in cluster analysis. Biometrics 35:169–181 Everitt BS, Landau S, Leese M (2001) Cluster analysis, 4th edn. Edward Arnold, London
- Schmatter SF (2011) Panel data analysis: a survey on model-based clustering of time series, Advanced Data Analysis and Classification, 5: 251-280.
- Vermunt JK (2010) Longitudinal research using mixture models. In: van Montfort K, Oud JHL, Satorra A (eds) Longitudinal research with latent variables, Chapter 4. Springer, Heidelberg, pp 119–152
